“Who wants to go to the pool?” seems like a simple question when you have two kids. By the time you have four kids, it becomes a diplomatic negotiation worthy of the United Nations.
During a recent family vacation, I started thinking about why this happens. If two people create X amount of complexity, then surely four people should create 2X complexity, right? It turns out that family dynamics follow much wilder mathematical rules...
Note: You may want to read this post with interactive visualizations.
When Things Scale Predictably (Linear Growth)
Some aspects of family travel do exactly what you’d expect—they scale in a nice, predictable way.
Take airline tickets. Six tickets cost about six times what one ticket costs. Each person you add increases your bill by roughly the same amount. It’s straightforward multiplication: n × cost per ticket. (Sure, six airline tickets can make your wallet weep, but at least the math is honest about it.)
Hotel room costs follow the same pattern. Two people need one room, four people need two rooms, six people need three rooms.
The math here is comforting in its simplicity:
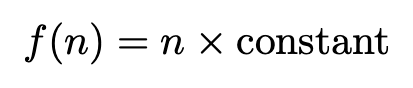
If only everything in family life worked this way.
When Relationships Multiply (Quadratic Growth)
But not everything scales so neatly. Managing interpersonal dynamics during our trip followed a completely different pattern.
Think about it this way—when you have just two people, there’s one relationship to manage. Add a third person, and suddenly you have three relationships (A-B, A-C, B-C). Add a fourth, and you’re up to six relationships.
The pattern follows quadratic growth, where each new person creates relationships with everyone already in the group:
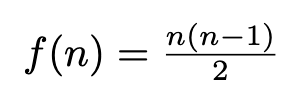
With our family of six, that’s (6 x 5) / 2 = 15 different interpersonal dynamics happening simultaneously:
- Who generally gets along and can be paired up without drama?
- Which relationship currently feels like a powder keg waiting to blow?
- Which combinations actually work well for different activities?
This showed up everywhere—from deciding who rides with whom in the car to managing the social dynamics during dinner conversations to figuring out which kids could share activities without driving each other (and us) crazy.
Each additional family member doesn’t just add one more person to consider—they add new relationships with everyone else already in the group. It’s why family gatherings can feel exponentially more complex even when you’re just adding one more cousin or grandparent to the mix.
When Decisions Spiral (Exponential Growth)
The real eye-opener came during our daily activity planning. Group decision-making doesn't just get a little harder with more people—it becomes exponentially more complex.
When just my partner and I were deciding between pool and museum, we had 4 possible scenarios:
- We both want pool ✅
- I want pool, partner wants museum ❌
- I want museum, partner wants pool ❌
- We both want museum ✅
That’s 4 scenarios to navigate, which shows exponential growth:
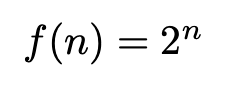
With our full family of six, each person could have “agree” or “disagree” positions on any proposed activity, creating 2⁶ = 64 possible opinion combinations.
But wait, it gets worse. Now you’re not just managing opinions—you’re managing coalitions:
- The pool faction vs. the museum faction
- The “let’s split up” group vs. the “stay together” group
- The inevitable “what about the aquarium instead?” counter-proposal
Each additional family member doubles the number of potential disagreement patterns you might need to navigate.
When Everything Becomes Chaos (Factorial Growth)
But the real complexity explosion? That came from our sleeping arrangements.
We had three beds and six people, which meant pairing everyone up. Sounds straightforward until you realize there are 6!/(2! × 2! × 2!) = 90 different ways to arrange these sleeping combinations.
And that’s before you factor in all the human considerations:
- Who snores and who’s a light sleeper?
- Which kids get along well enough to share a bed?
- Who has different bedtimes?
Suddenly that “simple” bed assignment became a multi-dimensional nightmare.
But if you really want to see factorial growth in action, consider something as mundane as standing in line at airport security. How many different ways could our family of six arrange ourselves? 6! = 720 different line sequences.
The first person in line could be any of the 6 family members, the second person could be any of the remaining 5, the third could be any of the remaining 4, and so on. This is factorial growth:
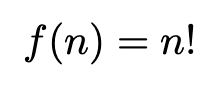
While we didn’t actually try all 90 sleeping combinations or 720 line arrangements (thankfully), it drove home how some types of complexity explode faster than others. If we’d had 7 family members instead of 6, we would have jumped from 720 to 5,040 possible line arrangements—seven times more complex for just one additional person.
So What Do I Do With This Information?
Honestly? Mostly just feel better knowing why family logistics are so exhausting. The mathematics of group dynamics means that adding one more person often makes things much more than “one person’s worth” of additional complexity.
Some problems scale predictably (linear stuff like costs), some scale with relationships (quadratic things like managing who gets along), some explode with choices (exponential group decisions), and some are just pure chaos (factorial arrangements).
The closest thing to wisdom I’ve gained? Sometimes the solution isn’t trying harder to manage complexity—it’s accepting that some problems grow faster than our ability to solve them. After all, 720 ways to stand in an airport line means there are 719 ways you’re not standing in line right now, and that’s perfectly fine.
Have similar stories? I’d love to hear about them.



